5.2.1 Geometrie eines Hexagons

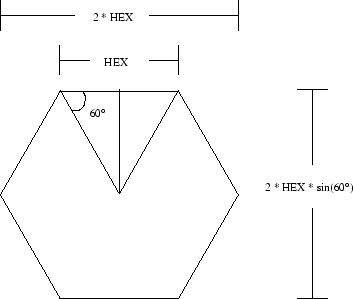
Die Poren im Gittersystem des zweidimensionalen Modells sind als Hexagone konzipiert. Die Größe wird durch die Seitenlänge HEX beschrieben, die auch dem Abstand vom Mittelpunkt zu einem der Eckpunkte entspricht (siehe Abb.5.1).

Abbildung 5.1: Geometrie eines Hexagons

Die Ausdehnung eines Hexagons in $x$- bzw. $y$-Richtung können durch folgende Formeln beschrieben werden:

$$\ \ \mathtt{HEX}_X = 2 * \mathtt{HEX}$$ (5.1)

$$\mathtt{HEX}_Y = 2 * \mathtt{HEX} * \sin(60^\circ)$$ (5.2)

Die Poren haben auch eine räumliche Ausdehnung in die $z$-Richtung, da sich die Angabe von Stoffkonzentrationen immer auf ein Standardvolumen beziehen. Es ist für das Simulationsergebnis unerheblich, wie groß die $z$-Komponente ist, da die Stoffflüsse und Abbaureaktionen linear proportional zum Porenvolumen sind (s.u.). Allerdings ist es am plausibelsten, eine räumliche Ausdehnung in der Größenordnung der Seitenlänge eines Hexagons zu wählen. Entsprechend wurde die Ausdehnung in $z$-Richtung auf 10cm gesetzt.

Das Volumen des Hexagons kann dann durch folgende Formel beschrieben werden:

$$\ \mathtt{HEX\_VOL} = \mathtt{HEX}_Z * \mathtt{HEX}^2 * \sin(60^\circ)$$ (5.3)

Die Diffusion zwischen zwei Porenzellen ist bezogen auf die Fläche mit der diese aneinandergrenzen. Sie ist definiert durch:

$$\ \ \mathtt{AREA} = \mathtt{HEX} * \mathtt{HEX}_Z$$ (5.4)

Mit HEX$_Z$ = 0,01m ergibt sich:

$$\mathtt{HEX\_VOL} = 0.03 * \mathtt{HEX}_Z * \sin(60^\circ)$$ (5.5)

und

$$\mathtt{AREA} = 0.01 * \mathtt{HEX}$$ (5.6)