6.3 Räumliche und zeitliche Auflösung

Ein großes Problem bei der Modellierung von Prozessen, die auf sehr kleinen Skalen stattfinden, ist die geeignete Wahl der räumlichen und zeitlichen Auflösung. Gerade bei der numerischen Approximation partieller Differentialgleichungen hängen die Ergebnisse oft von der Wahl des Maßstabs ab. Die Rechnerkapazität ist ein entscheidender Faktor, der eine höhere Auflösung verhindert. Die Aufgabe des Modellierers ist es, einen angemessenen Kompromiss zwischen numerischer Genauigkeit und rechnerischem Zeitaufwand zu finden. Der Einfluss einer Verdoppelung des Zeitintervalls auf die Ergebnisse ist sehr gering und deshalb nicht dargestellt. Allerdings treten bei einer Auflösung von CELL_HEIGHT = 0.05 m bei 16 Sekunden und bei einer Auflösung von 0.01 m schon bei 8 Sekunden so genannte Kompartiment-Overflows ein, d.h die Sauerstoffkonzentrationen werden negativ. Dabei handelt es sich um numerische Artefakte, die eine Überschätzung des diffusiven Flux zur Folge haben. Gerade bei höheren räumlichen Auflösungen müssen die Zeitschritte sehr kurz gewählt werden.

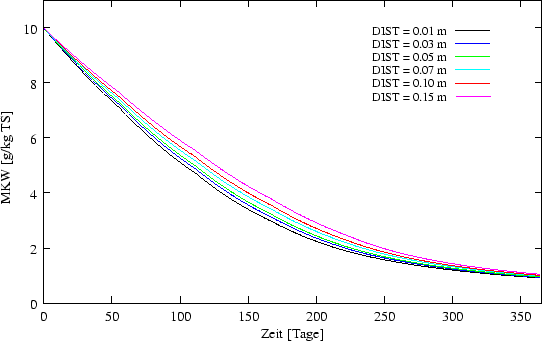
Die räumliche Auflösung selbst hat einen Einfluss auf die Geschwindigkeit des Abbaus. Bei kleineren Zellbreiten findet in der Gesamtmiete eine höhere Biodegradation statt. Dies ist durch eine höhere Differenzierung des Sauerstoffgradienten in der Miete zu erklären, die den Bereich mit O$_2$-Sättigung etwas erhöht. Hier handelt es sich um numerische Artefakte, die bei der Integration der Diffusionsgleichung bei niedrigeren räumlichen Auflösungen entsteht.

Abbildung: Simulation: Durchschnittliche Dieselölgehalte bei unterschiedlicher räumlicher Auflösung mit einer MKW-Anfangskonzentration von 10 g/kg Trockensubstanz. CELL_HEIGHT ist die Schichtdicke der Zellen im Halbkreis.