| (4.3) |

Das substratabhängige Wachstum wurde mathematisch von Monod (1949) beschrieben, und ist auch heute noch Grundlage vieler Modelle.
![]() ist das Substrat,
ist das Substrat, ![]() die maximale Wachstumsrate und
die maximale Wachstumsrate und ![]() ist die
Konzentration bei der
ist die
Konzentration bei der
![]() erreicht wird. Der resultierende Graph
ist eine hyperbolische Kurve, die sich mit zunehmender Substratkonzentration
erreicht wird. Der resultierende Graph
ist eine hyperbolische Kurve, die sich mit zunehmender Substratkonzentration
![]() annähert.
annähert.
Das Monod-Modell lässt verschiedene Vereinfachungen zu. Wenn ![]() ist,
kann
ist,
kann ![]() durch
durch ![]() angenähert werden. Die Zellteilungsrate ist dann
über einen großen Bereich hinweg konstant. Ist
angenähert werden. Die Zellteilungsrate ist dann
über einen großen Bereich hinweg konstant. Ist ![]() , geht auch das
Wachstum gegen Null.
, geht auch das
Wachstum gegen Null.
Der Substratabbau kann abhängig von der Wachstumsrate und der Anzahl der metabolisierenden Organismen oder der Biomasse beschrieben werden. Dabei wird angenommen, dass jede Zelle im Durchschnitt gleich viel Substrat verwerten kann. Es können drei unterschiedlich Verlaufskinetiken der Biodegradation unterschieden werden (Alexander und Scow, 1989; vgl. Abb. 4.1):
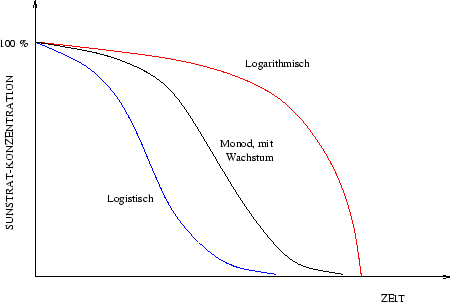 |
Ist
![]() , ergibt sich eine logarithmische Kinetik der Form
, ergibt sich eine logarithmische Kinetik der Form
Ist
![]() , wird das Wachstum mit zunehmendem Abbau immer geringer.
In diesem Fall ergibt sich eine logistische Kinetik. Dabei
steigt zunächst die Abbaurate mit der wachsenden Biomasse, aber mit sinkender
Substratmenge wird sie immer geringer und geht schließlich gegen
Null.
, wird das Wachstum mit zunehmendem Abbau immer geringer.
In diesem Fall ergibt sich eine logistische Kinetik. Dabei
steigt zunächst die Abbaurate mit der wachsenden Biomasse, aber mit sinkender
Substratmenge wird sie immer geringer und geht schließlich gegen
Null.
Im dritten Fall ist
![]() und der Abbau sowohl von der
Substratkonzentration als auch der Wachstumsrate abhängig. Diese Kinetik wird
Monod mit Wachstum genannt.
und der Abbau sowohl von der
Substratkonzentration als auch der Wachstumsrate abhängig. Diese Kinetik wird
Monod mit Wachstum genannt.
Auch hier nimmt die Abbaurate zunächst zu, um mit sinkender Substratkonzentration abzufallen.
Allen drei Kinetiken gemein ist die Tatsache, dass die initiale Bakterien- oder Pilzpopulation zunächst anwächst und sich die Abbaurate erhöht. In den Verlaufskurven der 35 Schadensfälle ist die Rate der Biodegradation allerdings zu Beginn der Sanierung maximal. Das kann daran liegen, dass die Kontaminationen nie frisch sind und sich die Biomasse schon auf ihrem höchsten Niveau befindet.
Die Monod-Gleichung kann das substratabhängige Wachstum von Bakterien-Reinkulturen mit sehr kleiner Populationsdichte zu Beginn des Abbaus unter optimalen Bedingungen beschreiben. Dazu zählen ausreichende Nährstoffversorgung, ständige Bioverfügbarkeit des Substrats oder ideale Außenparameter (pH, Temperatur).
Im Boden ist das Wachstum der Bakterien von vielen Randbedingungen abhängig, und es ist nicht zu erwarten, dass die Entwicklung der Biomasse mit den Laborbefunden vergleichbar ist. Vor allem sind Substrate im Boden nicht vollständig verfügbar, weil sie z.B an Oberflächen der Bodenpartikel sorbiert sind. Ebensowenig ist, wie diese Arbeit zeigt, mit einer ausreichenden Sauerstoffversorgung in allen Bodenarealen zu rechen. Und nicht zuletzt wachsen die ubiquitären MKW-Abbauer auf mehreren Substraten zugleich.
