
Wenn die Bakterienzelldichte zu Beginn der Sanierung relativ
zur Substratkonzentration sehr hoch ist, kann angenommen werden, dass die Biomasse nicht
wächst. Der Abbau wird dann durch die Substratsättigung an den Enzymen
kontrolliert. Dieser Zusammenhang kann mathematisch durch die
Michaelis-Menten-Kinetik beschrieben werden , die formal der
Monod - Funktion ähnelt, in der aber die Wachstumsrate ![]() durch die
Reaktionsrate
durch die
Reaktionsrate ![]() ersetzt wird.
ersetzt wird.
Wie oben können auch hier wieder verschiedene Fälle betrachtet werden.
 |
Wenn
![]() ist, kann
ist, kann ![]() durch
durch ![]() angenähert werden. Die
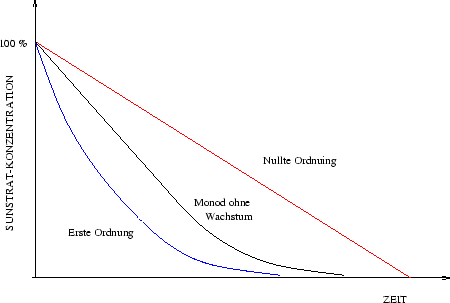
Abbaurate ist dann über die Zeit konstant und der Abbau folgt einer Kinetik
nullter Ordnung,
angenähert werden. Die
Abbaurate ist dann über die Zeit konstant und der Abbau folgt einer Kinetik
nullter Ordnung,
wobei ![]() die initiale und konstante Biomasse ist. Der Verlauf des Abbaus
ist linear, weil immer genügend Substrat vorhanden ist, um die vorhandenden
Enzymsysteme zu sättigen. Dieser Fall kann die Biodegradation in den 35
Schadensfällen nur zu Beginn der Sanierung beschreiben. Später limitiert die
Verfügbarkeit der Kohlenwasserstoffe den Abbau.
die initiale und konstante Biomasse ist. Der Verlauf des Abbaus
ist linear, weil immer genügend Substrat vorhanden ist, um die vorhandenden
Enzymsysteme zu sättigen. Dieser Fall kann die Biodegradation in den 35
Schadensfällen nur zu Beginn der Sanierung beschreiben. Später limitiert die
Verfügbarkeit der Kohlenwasserstoffe den Abbau.
Im anderen Extrem ist
![]() . Dann fällt die Abbaurate proportional zur
sinkenden Substratkonzentration und folgt einer Kinetik erster Ordnung:
. Dann fällt die Abbaurate proportional zur
sinkenden Substratkonzentration und folgt einer Kinetik erster Ordnung:
![]() ist die Reaktionskonstante 1.Ordnung und beschreibt die prozentuale Rate,
mit der das Substrat abgebaut wird.
ist die Reaktionskonstante 1.Ordnung und beschreibt die prozentuale Rate,
mit der das Substrat abgebaut wird.
Im dritten Fall ist
![]() und der Abbau sowohl von der
Substratkonzentration als auch von der Reaktionsrate abhängig. Dieser Zusammenhang
kann als Monod ohne Wachstum oder einfach
Michaelis-Menten-Kinetik bezeichnet werden.
und der Abbau sowohl von der
Substratkonzentration als auch von der Reaktionsrate abhängig. Dieser Zusammenhang
kann als Monod ohne Wachstum oder einfach
Michaelis-Menten-Kinetik bezeichnet werden.
Wie in Abbildung 4.2 dargestellt, folgt diese Kinetik zunächst einem Verlauf nullter Ordnung um schließlich in einen Abbau erster Ordnung überzugehen.
Diese Kinetik kann den Abbau der Mineralölkohlenwasserstoffe in den 35 Schadensfällen gut beschreiben und wurde daher in einer modifizierten Form im Modellansatz benutzt (vgl. Abschnitt 5.6).
Den Kinetiken ohne Biomassewachstum ist gemeinsam, dass die maximale Abbaurate zu Beginn der Sanierung erreicht wird. Nur bei der Funktion nullter Ordnung wird sie über die ganze Simulationsdauer auf diesem Level gehalten. In den beiden anderen Fällen tritt mit der Zeit eine Substrat-Limitierung ein, welche die Biodegradations-Rate senkt. Diese Konstrukte stimmen gut mit den empirischen Befunden überein.
