
Die Porenzellen werden durch gerichtete Diffusionsprozesse von der
Mietenoberfläche in den Boden hinein mit Sauerstoff versorgt. Bei
ausreichendem Porenluftvolumen ist Diffusion in der Gasphase der
Haupt-Transportprozess. Bei abnehmendem
![]() -Werten wird auch
die Luftdurchlässigkeit immer geringer. Diese Situation tritt vor allem bei
hohen Wassergehalten in feinkörnigen Böden ein. Dann sind immer weniger
kontinuierliche Luftpfade vorhanden, und der diffusive Transport von Sauerstoff
in der Porenluft kommt zum Erliegen [Huesemann and Truex, 1996]. O
-Werten wird auch
die Luftdurchlässigkeit immer geringer. Diese Situation tritt vor allem bei
hohen Wassergehalten in feinkörnigen Böden ein. Dann sind immer weniger
kontinuierliche Luftpfade vorhanden, und der diffusive Transport von Sauerstoff
in der Porenluft kommt zum Erliegen [Huesemann and Truex, 1996]. O![]() kann in so einer
Situation nur noch in der flüssigen Phase diffundieren. Der Netto-Transport
ist dann allerdings so gering, dass der aerobe Abbau von Kohlenwasserstoffen
zum Erliegen kommt. Im Fick'schen Gesetz wird der diffusive Flux
zwischen zwei Kompartimenten durch den effektiven Diffusionskoeffizienten und
den Konzentrationsgradienten der diffundierenden Substanz
kontrolliert.
kann in so einer
Situation nur noch in der flüssigen Phase diffundieren. Der Netto-Transport
ist dann allerdings so gering, dass der aerobe Abbau von Kohlenwasserstoffen
zum Erliegen kommt. Im Fick'schen Gesetz wird der diffusive Flux
zwischen zwei Kompartimenten durch den effektiven Diffusionskoeffizienten und
den Konzentrationsgradienten der diffundierenden Substanz
kontrolliert. ![]() wird im Modell durch eine mathematische Beziehung, die
von Millington (1959) entwickelt wurde, berechnet. Determinierend für die
Größe von
wird im Modell durch eine mathematische Beziehung, die
von Millington (1959) entwickelt wurde, berechnet. Determinierend für die
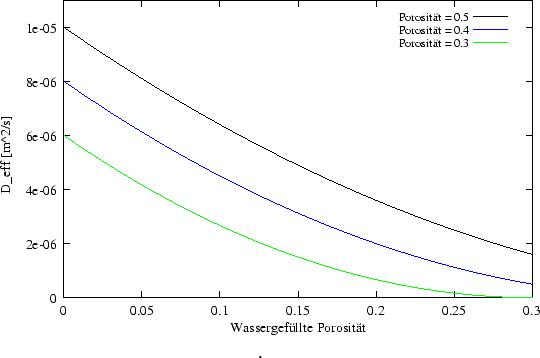
Größe von ![]() ist der Wassergehalt und die
Gesamtporosität. Abb. 7.1 zeigt exemplarisch die Werte für den
effektiven Diffusionskoeffizienten bei unterschiedlichen Porositäten und
Wassergehalten. Es gibt noch einige andere Algorithmen zur Berechnung von
ist der Wassergehalt und die
Gesamtporosität. Abb. 7.1 zeigt exemplarisch die Werte für den
effektiven Diffusionskoeffizienten bei unterschiedlichen Porositäten und
Wassergehalten. Es gibt noch einige andere Algorithmen zur Berechnung von
![]() , die sich außerhalb von Extrembedingungen aber annähernd
gleichen [Hillel, 1998].
, die sich außerhalb von Extrembedingungen aber annähernd
gleichen [Hillel, 1998].
 |
![]() bestimmt in der Diffusionsgleichung den Flux zwischen
zwei Zellen. Neben Änderungen bei der luftgefüllten Porosität reagiert er
recht empfindlich auf unterschiedliche Werte des Diffusionskoeffizienten in
freier Luft. Es gibt jedoch wenig Anlass, an den Literaturwerten für
bestimmt in der Diffusionsgleichung den Flux zwischen
zwei Zellen. Neben Änderungen bei der luftgefüllten Porosität reagiert er
recht empfindlich auf unterschiedliche Werte des Diffusionskoeffizienten in
freier Luft. Es gibt jedoch wenig Anlass, an den Literaturwerten für
![]() zu zweifeln, da diese empirisch gut belegt sind. Die Diffusion ist temperaturabhängig. Allerdings
ist der Effekt lange nicht so ausgeprägt wie bei anderen Transportmechanismen
wie Konvektion oder Advektion. Die Temperatur hat auch einen Einfluss auf die
Löslichkeit von Sauerstoff in Wasser. Bei steigenden Temperaturen verringert
sich die Henry-Konstante und damit die gelöste
O
zu zweifeln, da diese empirisch gut belegt sind. Die Diffusion ist temperaturabhängig. Allerdings
ist der Effekt lange nicht so ausgeprägt wie bei anderen Transportmechanismen
wie Konvektion oder Advektion. Die Temperatur hat auch einen Einfluss auf die
Löslichkeit von Sauerstoff in Wasser. Bei steigenden Temperaturen verringert
sich die Henry-Konstante und damit die gelöste
O![]() -Konzentration. Aufrund der Volumenausdehnung bei steigenden Temperaturen
verringert sich auch der Sauerstoffgehalt in der Luft. Im Modell hat O
-Konzentration. Aufrund der Volumenausdehnung bei steigenden Temperaturen
verringert sich auch der Sauerstoffgehalt in der Luft. Im Modell hat O![]() in
der Aussenluft eine Konzentration von
in
der Aussenluft eine Konzentration von
![]() ; das entspricht dem Wert bei 20°C. Ihre größte Bedeutung haben
Temperaturgradienten für die Geschwindigkeit des enzymatischen
Abbaus. Hauptsächlich aus diesem Grund wäre es wünschenswert, sie in das
Modell zu integrieren. Im Zuge einer solchen Erweiterung könnten auch
; das entspricht dem Wert bei 20°C. Ihre größte Bedeutung haben
Temperaturgradienten für die Geschwindigkeit des enzymatischen
Abbaus. Hauptsächlich aus diesem Grund wäre es wünschenswert, sie in das
Modell zu integrieren. Im Zuge einer solchen Erweiterung könnten auch ![]() und die Sauerstoffkonzentration entsprechend angepasst werden.
und die Sauerstoffkonzentration entsprechend angepasst werden.
Welchen Einfluss die Aggregatbildung auf die Sauerstoffdiffusion hat, ist noch nicht vollständig geklärt. Bei gleichem Wassergehalt könnte in Böden mit großem Anteil an Aggregaten eine höhere Diffusion stattfinden, weil die Makroporen dann trockener sind [Collin and Rasmuson, 1988]. Dies gilt aber wohl vor allem in tonigen Böden, wo kontinuierliche Luftpfade seltener sind als in Sand. Der Miteinbeziehung von Heterogenitäten in ein Diffusionsmodell macht nur dann Sinn, wenn entsprechende Daten über die Bodencharakteristika vorhanden sind. Bis auf weiteres ist es sinnvoll, Diffusion als statistisches Mittel in einer heterogenen Umgebung zu modellieren.
